Matemático Resolve o Quebra-Cabeças do Sofá Móvel de Longa Duração

Crédito: Depositphotos

Quando se trata de mudar móveis, os matemáticos não são normalmente as primeiras pessoas que pensamos consultar. E porque é que haviam de ser? Durante quase seis décadas, não conseguiram responder de forma definitiva se o seu elegante sofá de três lugares conseguia fazer aquela curva complicada para o corredor do seu apartamento.

No entanto, Jineon Baek, um entusiasta da matemática da Universidade de Yonsei, na Coreia do Sul, poderá mudar essa perceção. Baek revelou uma prova inovadora de 100 páginas que aborda exatamente este enigma, salvando-nos potencialmente de inúmeras frustrações no dia da mudança. O seu trabalho oferece uma solução para um quebra-cabeças que tem fascinado a comunidade matemática durante anos: como escolher mobiliário que não fique preso a meio de uma escadaria estreita ou numa esquina afiada.

As origens do problema do sofá móvel

O problema, formalmente introduzido pelo matemático austríaco-canadiano Leo Moser em 1966, aborda uma questão aparentemente simples: qual é o maior objeto bidimensional que pode manobrar através de uma curva em forma de L num corredor de uma unidade de largura?

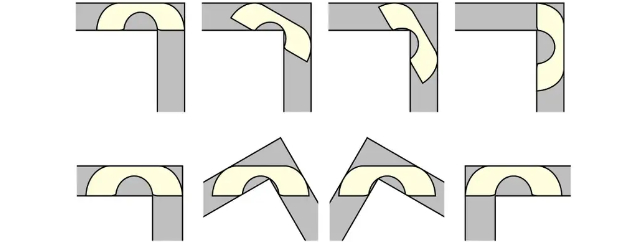
Also known as the ‘you swear it’s the last time you ever help a friend move’ problem. (Baek, arXiv, 2024)

Uma cadeira com uma unidade quadrada pode deslizar sem esforço, mas um retângulo com duas unidades quadradas vai certamente ficar preso. Algo mais comprido? Esqueça; é aí que fica. As coisas tornam-se mais complicadas quando se pensa em mobiliário com formas irregulares – pense nos designs do IKEA com nomes de personagens de fantasia, com curvas que se assemelham a receptores de telefone da velha guarda.

Em 1968, o matemático britânico John Hammersley propôs uma forma feita de um semicírculo unido a um quadrado com um entalhe semicircular. Este desenho, segundo ele, poderia passar pelo canto se tivesse uma área de até 2,2074 unidades. Ele também estabeleceu um limite superior, observando que nenhuma forma maior que 2,8284 unidades poderia caber.

Décadas mais tarde, em 1992, Joseph Gerver, da Universidade de Rutgers, aperfeiçoou o conceito de Hammersley. Ao suavizar algumas arestas e introduzir curvas adicionais, Gerver descobriu uma forma com uma área ligeiramente superior a 2,2195 unidades. A sua solução foi considerada “localmente óptima”, o que significa que era o melhor resultado dentro dos limites daquela forma específica.

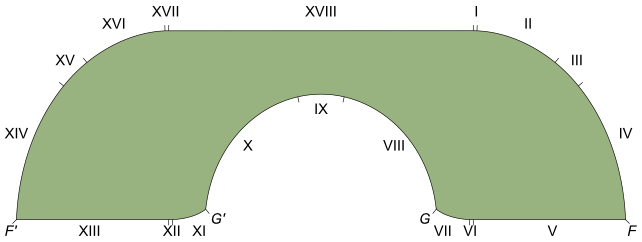
O sofá da Gerver tem uma série complexa de curvas. Também está disponível em azul celeste e amarelo canário. (TilmannR/Wikimedia Commons/PD)

Mas a procura de uma resposta definitiva persistiu. Sem uma fórmula universal para ter em conta todos os designs possíveis de sofás, não havia garantias de que um sofá ligeiramente maior ou com curvas diferentes não funcionasse. Em 2018, os investigadores Yoav Kallus e Dan Romik alargaram ainda mais os limites utilizando técnicas assistidas por computador, sugerindo que um sofá poderia, teoricamente, ter até 2,37 unidades.

A recente descoberta de Baek baseia-se num conceito matemático avançado conhecido como função injetiva. Esta abordagem permitiu-lhe mapear e analisar as propriedades do design do sofá de Gerver, expandindo sistematicamente as dimensões para confirmar o tamanho máximo possível. A sua conclusão? O sofá ideal para um corredor de uma unidade de largura e uma curva em forma de L é, de facto, de 2,2195 unidades, correspondendo à proposta de Gerver de 1992.

Embora as descobertas de Baek ainda não tenham sido submetidas a uma revisão por pares, podem representar o capítulo final deste desafio matemático de longa data – pelo menos para cenários de uma só esquina. Se o seu corredor tiver uma segunda curva na direção oposta, talvez seja necessário considerar o “sofá ambidestro” de Romik.

Leia o Artigo Original: Science Alert

Leia mais: Um Químico Inesperado pode ser a Causa das Dores de Cabeça causadas pelo Vinho Tinto