10 Novas Provas do Teorema de Pitágoras a partir de uma Questão Bônus

Crédito: Pixabay
Há muito tempo, considerava-se impossível usar a trigonometria para demonstrar um teorema que é fundamental para os princípios trigonométricos, pois isso cria uma falácia lógica de raciocínio circular ao tentar provar um conceito usando o próprio conceito.
“Não existem provas trigonométricas porque todas as fórmulas fundamentais da trigonometria são baseadas na validade do teorema de Pitágoras”, afirmou o matemático Elisha Loomis em 1927.
O que começou como uma questão bônus em um concurso de matemática do ensino médio resultou em impressionantes 10 novas provas do antigo teorema de Pitágoras.
O Dilema do Raciocínio Circular nas Provas Trigonométricas
No entanto, há muito tempo, foi considerado impossível usar a trigonometria para provar um teorema que sustenta os conceitos trigonométricos, pois isso leva a uma falácia lógica de raciocínio circular ao tentar validar um conceito usando ele mesmo.

“Ne’Kiya Jackson (à esquerda) e Calcea Johnson (à direita). (Calcea Johnson)
“Não existem provas trigonométricas porque todas as fórmulas fundamentais da trigonometria dependem da veracidade do teorema de Pitágoras”, escreveu o matemático Elisha Loomis em 1927.
Teorema de Pitágoras
O teorema de Pitágoras explica a relação entre os três lados de um triângulo retângulo. Este teorema é extremamente valioso em engenharia e construção e foi utilizado por pessoas séculos antes de ser formalmente associado a Pitágoras. Alguns argumentam que pode ter sido até mesmo aplicado na construção de Stonehenge.
O teorema é um princípio fundamental na trigonometria, que se concentra principalmente no cálculo das relações entre os lados e ângulos dos triângulos. Você provavelmente se lembra de ter aprendido a equação (a² + b² = c²) durante seus anos escolares.
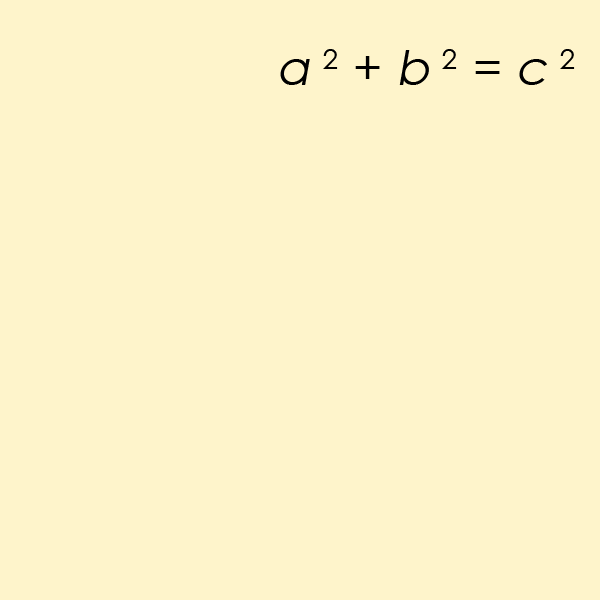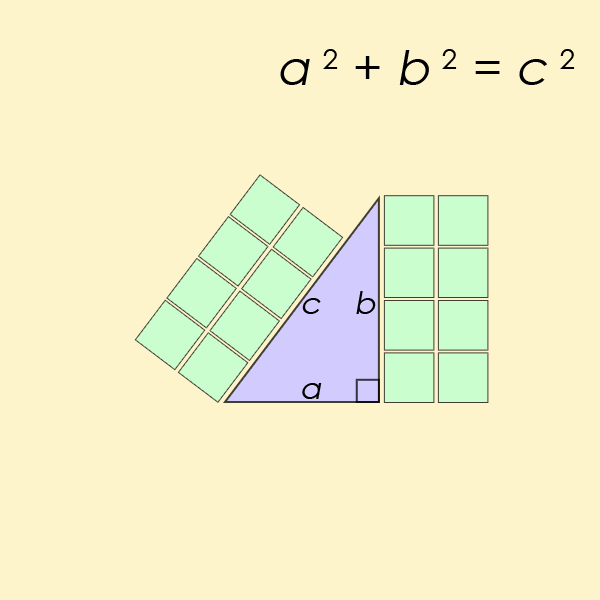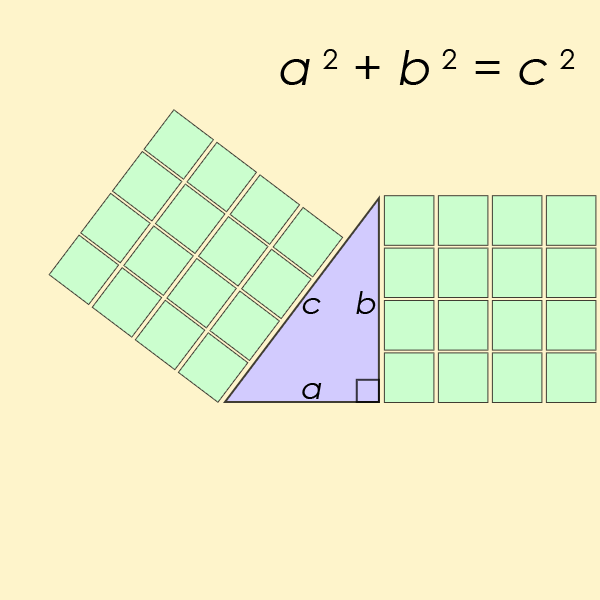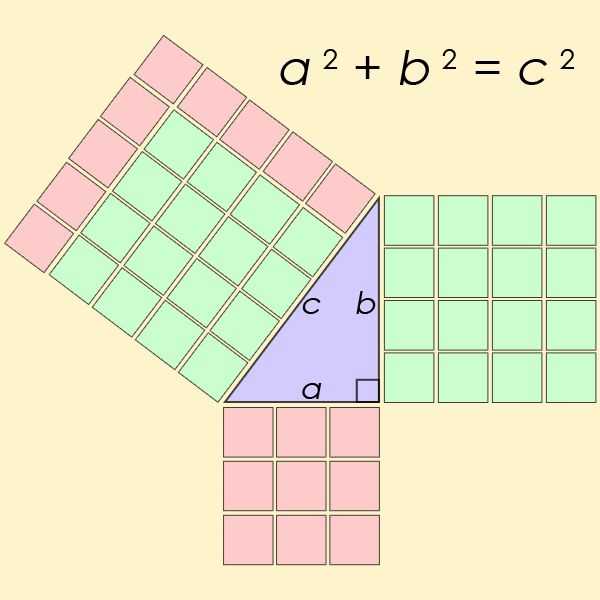
“Teorema de Pitágoras visualizado. (AmericanXplorer13/Wikimedia/CC BY-SA 3.0)”
“Os alunos podem não estar cientes de que duas versões conflitantes da trigonometria compartilham a mesma terminologia”, explicam Jackson e Johnson.
“Em tal situação, entender a trigonometria pode parecer como tentar decifrar uma imagem onde duas imagens distintas estão sobrepostas.”
No entanto, ao esclarecer essas duas variações relacionadas, mas distintas, Jackson e Johnson elaboraram novas soluções usando a Lei dos Senos, evitando efetivamente o raciocínio circular direto. Jackson e Johnson detalham esse método em seu novo artigo, reconhecendo que a distinção entre abordagens trigonométricas e não trigonométricas é um tanto subjetiva.
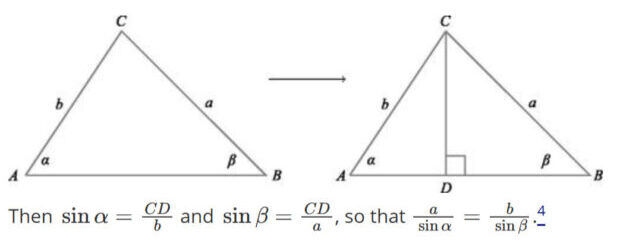
“A Lei dos Senos mostra como os ângulos podem ser usados para calcular a altura do triângulo (CD).. (Jackson & Johnson, Amer. Math. Monthly, 2024)”.
Novas Provas Trigonométricas
Eles também destacam que, de acordo com sua definição, outros dois matemáticos, J. Zimba e N. Luzia, também provaram o teorema usando trigonometria, desafiando alegações anteriores de que isso era impossível.
Na verdade, em uma de suas provas, os dois alunos levaram a definição de cálculos envolvendo triângulos ao limite, preenchendo um triângulo maior com sequências de triângulos menores e empregando cálculo para determinar as medidas dos lados do triângulo original.
“É algo que eu nunca encontrei antes”, disse Álvaro Lozano-Robledo, um matemático da Universidade de Connecticut, em uma entrevista com Nikk Ogasa, da Science News.
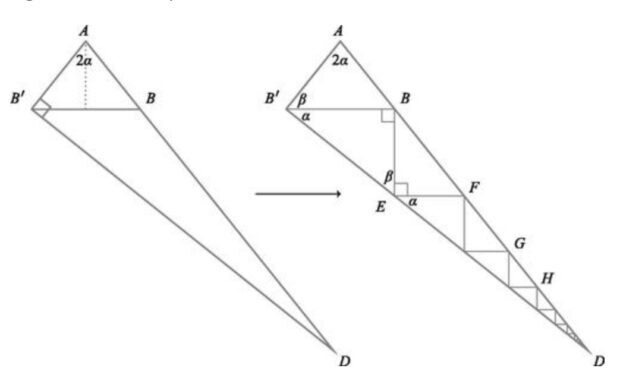
“Dividindo seus triângulos retângulos em mais triângulos, a equipe encontrou maneiras novas de calcular as propriedades do triângulo original. (Jackson & Johnson, Amer. Math. Monthly, 2024).”
No total, Jackson e Johnson apresentam uma prova para triângulos retângulos com dois lados iguais e quatro provas adicionais para triângulos retângulos com lados desiguais, deixando pelo menos mais cinco para “o leitor curioso explorar”.
“Ter um artigo publicado em uma idade tão jovem é verdadeiramente impressionante”, observa Johnson, que atualmente está estudando engenharia ambiental. Jackson está estudando farmácia.
Para concluir, “As descobertas deles destacam o potencial de novas perspectivas dos estudantes na área”, diz Della Dumbaugh, editora-chefe da revista onde seu trabalho foi publicado.
Leia o Artigo Original Science Alert










