Enquanto se filmava se preparando para um trabalho recentemente, TikTok individual @gracie. porco aprofundou-se muito nos antigos fundamentos da matemática e também descobriu a verdadeira joia da questão:

Como uma pessoa pode desenvolver um conceito como álgebra?

Ela também perguntou para que o velho filósofo grego Pitágoras poderia ter usado a matemática e outras preocupações que giram em torno do antigo problema de se a matemática é “real” ou algo que os seres humanos compreendem.

Muitos reagiram adversamente ao post, mas outros — consistindo de matemáticos como eu — localizaram as investigações de forma bastante informativa.

A matemática é real?

Teóricos, assim como matemáticos, discutem sobre isso há séculos. Alguns acreditam que a matemática é universal; outros o consideram tão real quanto qualquer outra coisa que os humanos desenvolveram.

Obrigado a @gracie. Ham, os clientes do Twitter agora se inscreveram fortemente no debate.

De um ponto de vista, a matemática é uma linguagem universal usada para explicar o globo que nos rodeia. Por exemplo, duas maçãs mais três maçãs são constantemente cinco maçãs, apesar do seu ponto de vista.

Mas a matemática também é uma linguagem usada pelos humanos, portanto, não é independente da cultura. A história nos revela que várias culturas tinham a sua própria compreensão da matemática.

No entanto, muito desse antigo entendimento está perdido. Em quase todas as culturas antigas, algumas mensagens dispersas são tudo o que resta do seu conhecimento científico.

No entanto, existe uma sociedade antiga que deixou uma grande riqueza de mensagens.

Álgebra babilónica

Enterrados nos desertos do Iraque moderno, os tablets de argila da antiga Babilónia sobreviveram sem danos por cerca de 4.000 anos.

Essas tabuinhas são gradualmente equiparadas, e também o que descobrimos até agora é que os babilónios eram pessoas funcionais que eram muito numeradas e sabiam como consertar problemas avançados com números.

A matemática deles diferia da nossa, no entanto. Eles não utilizaram nenhum ou números negativos. Eles também mapearam o movimento dos planetas sem usar cálculos como fazemos.

De importância específica para @gracie. A preocupação de ham com relação aos primórdios da álgebra é que eles entenderam que os números 3, 4 e 5 representam os comprimentos dos lados e da diagonal de um retângulo. Eles da mesma forma reconheceram que esses números agradavam à relação essencial 3 ² + 4 ² = 5 ² que garante que os lados sejam perpendiculares.

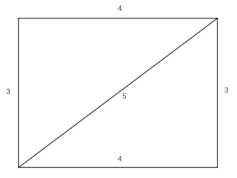
Nenhuma tese foi danificada (ou utilizada) na construção e construção desta forma retangular.

Os babilónios fizeram tudo isso sem princípios algébricos contemporâneos. Nós revelaríamos uma variação muito mais básica da mesma sugestão usando a tese de Pitágoras: qualquer triangular em ângulo reto com lados de tamanho e, bem como be hipotenusa c, satisfaz a ² + b ² = c ². O ponto de vista babilónico deixa de fora variáveis ​​algébricas, teoremas, axiomas e evidências, não porque eles estivessem alheios, no entanto, porque essas ideias ainda não haviam sido criadas. Simplificando, essas construções sociais começaram mais de 1.000 anos depois, na antiga Grécia. Os babilónios alegre e produtivamente fizeram matemática e resolveram problemas sem nenhuma dessas ideias razoavelmente contemporâneas.

Para que foi tudo isso?

@gracie. ham, adicionalmente, pergunta como Pitágoras gerou o seu teorema. A resposta curta é: ele não o fez.

Pitágoras de Samos (c. 570 – 495 aC) provavelmente ouviu falar do conceito que atualmente relacionamos a seu nome enquanto ele permaneceu no Egito. Ele pode ter sido o indivíduo a apresentá-lo à Grécia, mas não sabemos.

Pitágoras não utilizou a sua tese para nada prático. Ele estava interessado principalmente em numerologia e necromancia de números, em vez das aplicações da matemática.

Saiba mais: crianças interessadas: como a matemática foi descoberta? Quem inventou os números e os regulamentos?

Por outro lado, os babilónios podem muito bem ter utilizado o seu conhecimento de triangular retângulo para objetivos mais concretos, embora não saibamos. Temos provas da Índia e Roma antigas revelando que as dimensões 3-4-5 foram usadas como um método primário, mas eficaz, para produzir ângulos apropriados na construção e construção de igrejas espirituais e avaliação.

Sem ferramentas modernas, como ajustar os ângulos de forma perfeita? Antigas mensagens religiosas hindus fornecem instruções para fazer uma igreja de fogo em forma de retângulo utilizando o arranjo 3-4-5 com lados de tamanhos 3 e 4 e diagonais de tamanho 5. Essas medidas garantem que o altar tenha ângulos apropriados em cada canto.

Enormes preocupações

No século XIX, o matemático alemão Leopold Kronecker afirmou: “Deus fez os inteiros. Tudo o mais é trabalho dele”. No mínimo, eu concordo com esse sentimento para os inteiros positivos — os números inteiros com os quais contamos — porque os babilónios não dependiam de nenhum número ou de números negativos.

A matemática vem a acontecer há muito tempo — muito antes da velha Grécia e Pitágoras.

É genuíno? A maioria das culturas concorda com relação a alguns fundamentos, como os inteiros positivos e também o triângulo retângulo 3-4-5. Quase tudo o mais na matemática é determinado pela sociedade em que vive.

Relacionados APG lança sua certificação para representantes em viagem