O que é teoria dos jogos?
No sentido matemático, um jogo é um cenário no qual os jogadores fazem escolhas racionais de acordo com regras definidas para obter algum tipo de benefício. A teoria dos jogos é o ramo da matemática que se concentra na análise desses videogames. A teoria dos jogos pode ser dividida em duas subdisciplinas principais: teoria clássica dos jogos e teoria combinatória dos jogos.
A teoria clássica dos jogos pesquisa jogos nos quais os jogadores se movem, apostam ou planejam tudo de uma vez. Como resultado, os jogadores frequentemente ficam alheios a facetas específicas do videogame. Os jogadores desses videogames têm maior probabilidade de confiar em previsões e possibilidades devido à falta de detalhes. As instâncias incluem pôquer de cassino ou pedra, papel, tesoura.
Por outro lado, a teoria dos jogos combinatórios é o estudo de jogos para dois jogadores em que cada jogador tem pleno conhecimento de todas as facetas do videogame ao longo de toda a jogabilidade. Esses jogos geralmente são jogados em uma base turn-by-turn e normalmente não envolvem componentes de instâncias aleatórias consistem em xadrez ou damas. Além disso, os videogames combinatórios são considerados imparciais se todos os jogadores tiverem o mesmo conjunto de ações possíveis em cada colocação. Caso contrário, o videogame é considerado partizan.
Classificação dos Jogos
Além de ambas as categorias fornecidas, os jogos podem ser identificados em uma seleção de métodos. Entre uma das mais aparentes está a categorização de um jogo pelo número de jogadores. É comum descrever um videogame como um videogame de n pessoas, em que n é um número inteiro maior ou igual a 1 que representa o número de jogadores chamados para ingressar em um determinado videogame.
A ordem em que os jogadores se movem (ou não) é outra maneira simples de classificar os videogames. Todos os jogadores fazem seus movimentos ao mesmo tempo em um videogame simultâneo. Ao contrário, em um videogame consecutivo, apenas um jogador pode se mover em qualquer tipo de momento oferecido. Alguns jogos nem sempre se enquadram em uma dessas classificações.
Os jogos também podem ser classificados com base nos lucros possíveis completos. Um videogame de soma constante ou jogo de soma zero é aquele em que a quantidade de ganhos possíveis permanece contínua, não importa o que os jogadores recebam; ou seja, a soma dos pagamentos obtidos por alguns jogadores deve ser igual ao número de perdas dos outros jogadores. No Texas Hold ’em, por exemplo, os jogadores competem por uma quantidade infinita de dinheiro. As escolhas de cada jogador não afetam os ganhos oferecidos em videogames de soma variável, no entanto, os ganhos gerais disponíveis podem se transformar dependendo das ações dos pagadores. A situação do detido é um exemplo de videogame de soma variável.
Os jogos de soma variável podem ser separados ainda mais em subgrupos aderentes: jogos cooperativos e não cooperativos. Os jogadores de jogos participantes podem fazer acordos vinculativos, como um acordo exequível, enquanto os jogadores de videogames não cooperativos podem não produzir quaisquer configurações vinculativas. Por exemplo, imagine que há duas pessoas, um vendedor e um comprador, querendo concluir uma transação comercial. Na medida em que tentam negociar um custo, as pessoas estão participando de um jogo não cooperativo se o comprador assinar um acordo consentindo em pagar um preço detalhado, depois disso acaba sendo um jogo participante.
Representação de Jogos
Existem vários métodos pelos quais podemos explicar os videogames. O primeiro que certamente discutiremos é conhecido como tipo abrangente. Nesta técnica, a série de opções feitas em um videogame é ilustrada utilizando uma árvore de jogo. A recompensa para cada uma das sequências possíveis é anotada no final de cada um dos últimos ramos considerando, como exemplo, a adesão à árvore parcial do jogo para um jogo de Tic-Tac-Toe entre 2 jogadores:
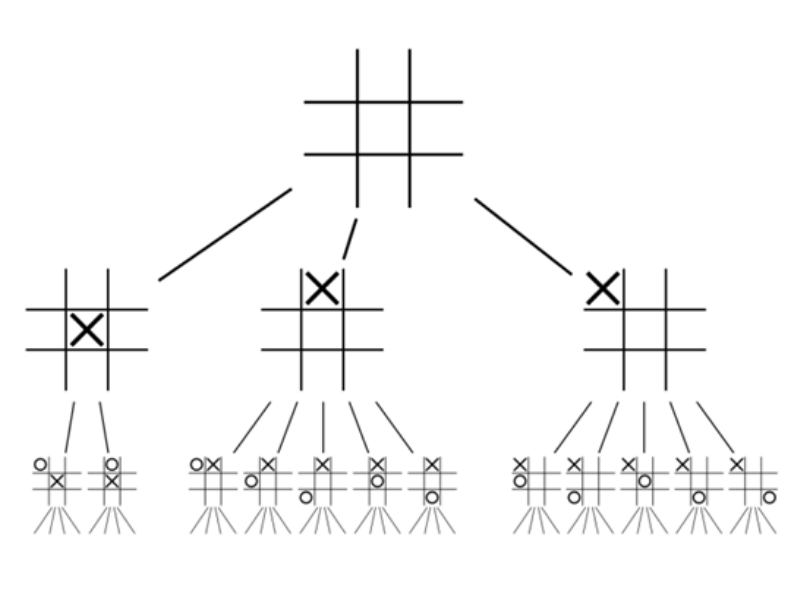
Considerando que as rotações e reflexos são equivalentes, o jogador 1 tem três etapas possíveis; como previsto acima, as possíveis realocações do Jogador 2 mudam, contando com a opção feita pelo Jogador 1. Se nós prolongássemos a árvore, sem dúvida veríamos quais movimentos o Jogador 1 poderia fazer em conformidade com a decisão do Jogador 2. Poderíamos desenhar uma árvore total para ver todos os resultados viáveis de todas as séries de movimentos possíveis. Observe que o tipo substancial também pode ser utilizado para explicar jogos sincronizados, usando linhas apressadas para mostrar que um jogador não sabe em qual nó está.
Embora os jogos de vídeo podem ser validamente descritos em forma ampla, eles podem ser mais claramente descritos usando o tipo normal, também conhecido como forma crítica. Portanto, o tipo típico é extra normalmente usado para explicar jogos de vídeo sincronizados (geralmente com dois jogadores). Na categoria normal, um jogo é representado usando uma matriz que descreve os resultados para ambos os jogadores para qualquer combinação de movimentos. Por exemplo, leve em consideração a adesão à matriz que ilustra o jogo do dilema do detento.
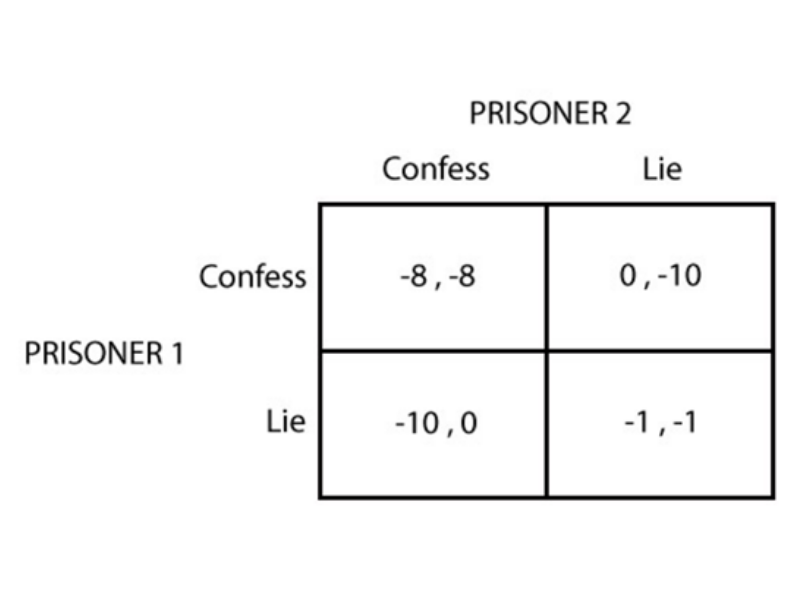
Os jogadores e todas as suas possíveis realocações são colocados em lados próximos da matriz. Os payoffs são posicionados dentro da matriz. Nesse caso, todas as retribuições são desfavoráveis, pois representam o tempo passado na prisão. A partir da matriz visualizada acima, vemos que se ambos os presos confessarem, cada um deles ficará 8 anos atrás das grades. Assim, um prisioneiro confessa, ele sai sem tempo de prisão, enquanto os vários outros jogadores precisam passar uma década atrás das grades. Se ambos os detidos existirem, cada um ficará apenas 1 ano atrás das grades.
Por último, os jogos cooperativos podem ser representados em tipos de funções particulares. Esta técnica é diferente das outras duas, pois examina o retorno para o grupo de jogadores como um todo, em vez de pensar nas decisões e benefícios individuais.
O Equilíbrio de Nash
O equilíbrio de Nash é uma ideia apresentada originalmente por um matemático americano, John Nash (1928-2015). Um videogame não cooperativo está em equilíbrio de Nash se nenhum jogador tiver a recompensa de alterar seu método de jogo privado após considerar os métodos de todos os outros jogadores. A questão do prisioneiro é um exemplo atemporal da estabilidade de Nash. A título de dica, o dilema do prisioneiro é uma circunstância em que 2 prisioneiros são condenados como cúmplices de um crime.
Os prisioneiros são colocados em confinamento solitário, portanto, eles não têm nenhuma técnica de conexão uns com os outros. Cada um deles é oferecido com o cumprimento da proposta:
- Se ambos admitirem, cada um deles passará oito anos atrás das grades.
- Então, um deles confessa que será solto, enquanto o outro vai passar dez anos na prisão.
- Se nenhum deles admitir, com certeza cada um vai investir 1 ano na prisão.
Este videogame está em equilíbrio de Nash quando os dois prisioneiros confessam. Porque? Pelo fato de que, nessas situações, nenhum dos presos se beneficia com a mudança de método. Se o Detento 1 mudasse sua estratégia e em vez disso ficasse quieto, depois disso ele obteria uma sentença de prisão mais longa do que certamente se admitisse, e o Detido 2 poderá ir embora sem punição. O prisioneiro 2 deve manter sua estratégia também pela mesma lógica. Embora a melhor abordagem para o grupo como um todo seja ambos ficarem quietos, individualmente os prisioneiros são muito melhores confessando, já que não têm outra maneira de entender o método do outro detido com antecedência, e ficar quietos enquanto o outro confessa levaria a dez anos de prisão.
O equilíbrio de Nash pode ser colocado em uma seleção de situações da vida real. Descreve, por exemplo, porque pescamos em excesso nos mares: Embora a pesca excessiva seja negativa para a comunidade em geral, seria um mau comportamento para uma empresa privada parar de pescar, pois esse negócio deixaria de ganhar dinheiro enquanto várias outras empresas continuam a pescar e, portanto, permanecer para ter lucro. A balança de Nash também pode ser usada em economia, batalha, política e muitos outros campos.
Referência: Brams, Steven J. e Morton D. Davis. “Teoria do jogo.” Encyclopædia Britannica, Encyclopædia Britannica, 2 de novembro de 2017






